2進数(Binary)、16進数(Hexadecimal)
ビット演算を理解するには2進数/16進数の理解が必要です。最初に以下の表を暗記します。2進数⇔16進数の変換はこれだけ覚えておけば16進数の一桁は4bitで表せるので桁が増えても変換できます。
※負数表現はまた別途
| 10進数 | 2進数 | 16進数 |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
上記を忘れた場合、ビットの値を考えれば計算できます。
0001(b) = 1
0010(b) = 2
0100(b) = 4
1000(b) = 8
よって
1111(b) = 1+2+4+8 = 15 = F(h)
※(b)は2進数の意、(h)は16進数の意
ビット演算の基本
AND
0 AND 0 = 0
0 AND 1 = 0
1 AND 0 = 0
1 AND 1 = 1
C言語での表現
A & B
OR
0 OR 0 = 0
1 OR 0 = 1
0 OR 1 = 1
1 OR 1 = 1
C言語での表現
A | B
XOR
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0
C言語での表現
A ^ B
NOT
NOT 0 = 1
NOT 1 = 0
C言語での表現
~A
右シフト
bitを右にずらすこと。
C言語での表現(n bit右シフト)
A >> n
左シフト
bitを左にずらすこと。
C言語での表現(n bit 左シフト)
A << n
算術シフトと論理シフト
ビットシフト演算には算術シフトと論理シフトがある。違いを理解するためには負数の扱いについて理解が必要です。
アセンブリ言語では算術シフトと論理シフトは明確に別のものとなっています。C言語ではunsignedの値に対しては論理シフト、signedの値に対しては算術シフトになります。
※色々間違いが起きやすいのでsignedの値に対してはビット演算は用いないのが無難です。また、浮動小数点型(floatとかdouble)にも論理演算は適用できません。
算術シフト
別名、符号付きシフト。符号ビットを維持したまま符号ビット以外のビットをシフトします。
例:符号付8bitの値「11000000(b)」を1bit右に算術シフトした場合、「11100000(b)」となります。
論理シフト
符号ビットを考慮せず全体をシフトします。
例:11000000(b)を 1bit右に論理シフトした場合、01100000(b)となります。
ビット演算の応用
原則は以下と覚えましょう。
- ANDはマスク、1のANDはビット抽出、0のANDはビットクリア
- ORはビットセット
- XORは部分反転
- NOTは全反転
- 右シフトは2のn乗の割り算
- 左シフトは2のn乗の掛け算
ビットマスク
ビットの論理演算を用いて特定のビットをON/OFFしたりビット状態を抽出したりすることです。
ビットの抽出
取り出すビットを1にした値でANDします。
例:3bit目を取り出す場合
A & 4
※4 = 0100(b)
A = 1110(b)の場合、1110(b) & 0100(b) = 0100(b)となります。
A = 1010(b)の場合、1010(b) & 0100(b) = 0000(b)となります。
ビットのセット
セットする(0→1にする)ビットを1にした値でORします。
例:3bit目をセットする場合
A | 4
※4 = 0100(b)
A = 0101(b)の場合、0101(b) | 0100(b) = 0101(b)となります(もともセットされた状態なので変化なし)。
A = 0001(b)の場合、0001(b) | 0100(b) = 0101(b)となります。
ビットのクリア
クリアする(1→0にする)ビットを0にした値でANDします。
例:3bit目をクリアする場合
A & 0xB
※B(h) = 1011(b)
以下でも同様です。
A & ~4
※~4 = ~0100(b) = 1011(b) = B(h)
A = 1110(b)の場合、1110(b) & 1011(b) = 1010(b)となります。
A = 1010(b)の場合、1010(b) & 1011(b) = 1010(b)となります(もともとクリアされた状態なので変化なし)。
※全てWindows 10の電卓(プログラマー電卓モード)で実際の演算を試すことができます。
C言語による演習
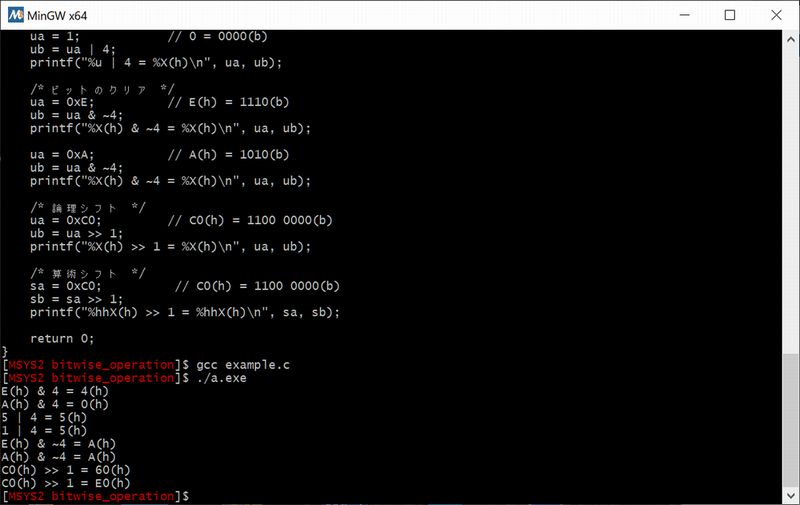
以下のプログラムを実行して結果を確認し理解しましょう。
#include <stdio.h>
int main()
{
signed char sa,sb;
unsigned char ua,ub;
/* ビットのマスク */
ua = 0xE; // E(h) = 1110(b)
ub = ua & 4;
printf("%X(h) & 4 = %X(h)\n", ua, ub);
ua = 0xA; // A(h) = 1010(b)
ub = ua & 4;
printf("%X(h) & 4 = %X(h)\n", ua, ub);
/* ビットのセット */
ua = 5; // 5 = 0101(b)
ub = ua | 4;
printf("%u | 4 = %X(h)\n", ua, ub);
ua = 1; // 0 = 0000(b)
ub = ua | 4;
printf("%u | 4 = %X(h)\n", ua, ub);
/* ビットのクリア */
ua = 0xE; // E(h) = 1110(b)
ub = ua & ~4;
printf("%X(h) & ~4 = %X(h)\n", ua, ub);
ua = 0xA; // A(h) = 1010(b)
ub = ua & ~4;
printf("%X(h) & ~4 = %X(h)\n", ua, ub);
/* 論理シフト */
ua = 0xC0; // C0(h) = 1100 0000(b)
ub = ua >> 1;
printf("%X(h) >> 1 = %X(h)\n", ua, ub);
/* 算術シフト */
sa = 0xC0; // C0(h) = 1100 0000(b)
sb = sa >> 1;
printf("%hhX(h) >> 1 = %hhX(h)\n", sa, sb);
return 0;
}実行結果は以下の通りです。
E(h) & 4 = 4(h) A(h) & 4 = 0(h) 5 | 4 = 5(h) 1 | 4 = 5(h) E(h) & ~4 = A(h) A(h) & ~4 = A(h) C0(h) >> 1 = 60(h) C0(h) >> 1 = E0(h)


コメント